ballqs 님의 블로그
[Java] 프로그래머스 문제 - 점 찍기 본문
오늘 풀어본 문제는 프로그래머스의 점 찍기 라는 문제를 풀어보았다.
애초에 어떻게 접근해야할지 감도 못잡고 있다가 같이 공부중인 분이 힌트를 줘서 진행이 가능해졌다.
문제 설명
이 문제는 x축과 y축이 직교하는 좌표명면에서 k 값과 d 값이 주어지면 다음과 같이 점을 찍는다.
- 원점(0, 0)으로부터 x축 방향으로 a*k(a = 0, 1, 2, 3 ...), y축 방향으로 b*k(b = 0, 1, 2, 3 ...)만큼 떨어진 위치에 점을 찍습니다.
- 원점과 거리가 d를 넘는 위치에는 점을 찍지 않습니다.
이는 좌표명면에 d 반지름의 원안에 k라는 간격만큼 점을 얼마나 찍을수 있는지 알아보기 위한 문제이다.
제한 조건
- 1 ≤ k ≤ 1,000,000
- 1 ≤ d ≤ 1,000,000
입출력 예
| k | d | result |
| 2 | 4 | 6 |
| 1 | 5 | 26 |
풀이과정
주어지는 d가 원의 반지름 길이라고 생각하여 원을 그린 후 범위 내에서 찍히는 점을 구하는 문제로 접근했다.
이를 풀기 위해선 피타고라스의 정리를 이용해서 풀어보고자 했다.
피타고라스의 정리는 누구나 배웠다 시피... c^2 = b^2 + a^2 공식이다. (티스토리에선 깔끔하게 안써지네 -_-)
이를 반전해서 보게 되면 c^2 - b^2 = a^2 라는 것이고 여기서 a^2를 루트하면 a값을 알수있다.
여기서 k만큼의 간격만큼 찍는거기때문에 나누기 처리하면 문제 없었다.
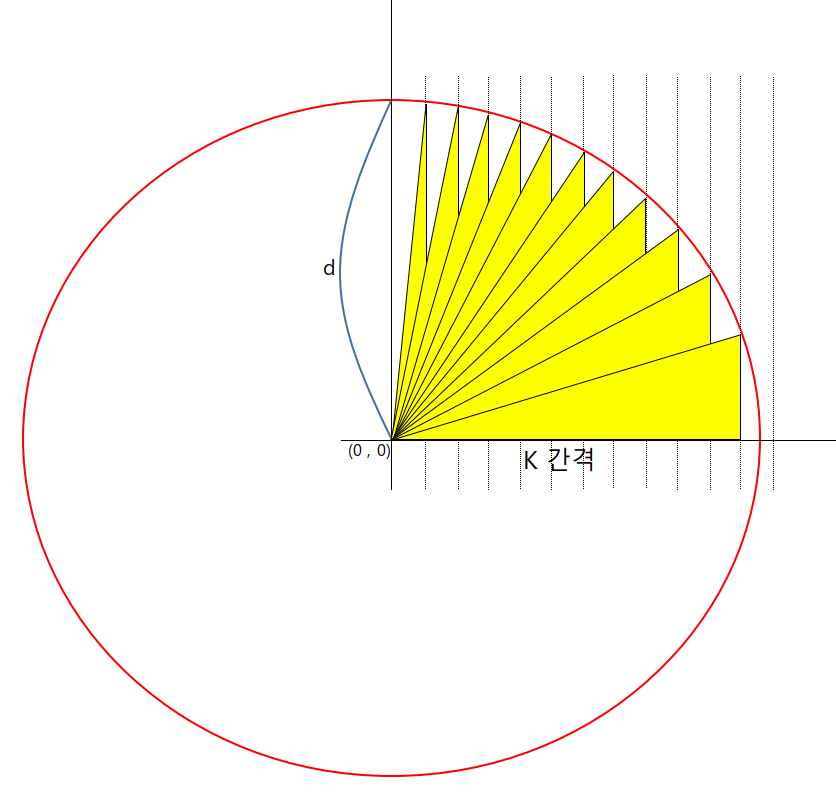
그림으로 보면 d의 길이를 고정으로 주고 k간격만큼 이동해서 높이를 구하는 방식으로 진행한 것이다.
코드
class Solution {
public long solution(int k, int d) {
long answer = 0;
// x^2 + y^2 = d^2
// x와 y가 변동이되고 d^2보다 작으면 점이 찍힌다.
// y(길이 완성) = 루트(d^2 - x^2) / k = 개수 0를 포함하기 위한 + 1
for (int i = 0; i <= d; i+=k) {
answer += (int) Math.sqrt(Math.pow(d , 2) - Math.pow(i , 2)) / k + 1;
}
return answer;
}
}'코딩 공부 > Java' 카테고리의 다른 글
| [Java] 프로그래머스 문제 - 미로 탈출 (0) | 2024.11.27 |
|---|---|
| [Java] Proxy 패턴이란? (0) | 2024.09.24 |
| [Java] Stack를 활용한 DFS 알고리즘으로 푼 문제 (0) | 2024.08.16 |
| [Java] 투 포인터(Two Pointer) 알고리즘이란? (0) | 2024.08.13 |
| [Java] Comparator compare() 과 Comparable compareTo() (0) | 2024.08.06 |




