ballqs 님의 블로그
[Java] 투 포인터(Two Pointer) 알고리즘이란? 본문
투 포인터(Two Pointer) 이란?
배열이나 리스트에서 두 개의 포인터를 사용하여 특정 조건을 만족하는 부분 구간을 효율적으로 탐색하는 알고리즘이다.
일반적으로 배열이나 리스트가 정렬되어 있을때 사용한다.
두 개의 포인터는 보통 양 쪽 끝으로 시작하여 각각 탐색하면서 특정 조건을 만족하는지 검증한다.
다만! 한 쪽 방향에서 동시에 시작하는 경우도 있는데 이는 해당 배열의 합과 차를 통해 특정 조건이 만족하는지 검증한다.
투 포인터의 문제 적용
프로그래머스 문제를 풀다가 이런 문제를 접했다.
연속된 부분 수열의 합 이라는 문제이다.
문제 설명
내림차순으로 정렬된 배열이 주어질 때 특정 조건을 만족하는 수열을 찾는 문제이다.
주어진 k값이 있고 배열의 연속된 부분의 합이 k와 같으면 해당 포인터들의 index를 반환하면 되는 문제이다.
단! 두 개의 포인터의 길이가 짧아야 한다.
제한사항
- 5 ≤ sequence의 길이 ≤ 1,000,000
- 1 ≤ sequence의 원소 ≤ 1,000
- sequence는 비내림차순으로 정렬되어 있습니다.
- 5 ≤ k ≤ 1,000,000,000
- k는 항상 sequence의 부분 수열로 만들 수 있는 값입니다.
입출력 예
| sequence | k | result |
| [1, 2, 3, 4, 5] | 7 | [2, 3] |
| [1, 1, 1, 2, 3, 4, 5] | 5 | [6, 6] |
| [2, 2, 2, 2, 2] | 6 | [0, 2] |
| [1, 2, 2, 2, 3, 3, 3] | 8 | [3, 5] |
| [5, 6, 7, 8] | 11 | [0, 1] |
| [1, 1, 1, 1, 1, 5] | 5 | [5, 5] |
입출력 예 설명
입출력 예 #2
[1, 1, 1, 2, 3, 4, 5]에서 합이 5인 연속된 부분 수열은 [1, 1, 1, 2], [2, 3], [5]가 있습니다. 이 중 [5]의 길이가 제일 짧으므로 해당 수열의 시작 인덱스와 마지막 인덱스를 담은 [6, 6]을 반환합니다.
풀이 과정
이 문제는 제한 조건만 봐도 이중 for문으로 찾는 방법에는 시간초과가 날 것이 안봐도 훤하다.
그래서 투 포인터 알고리즘을 사용하려고 한다. 2개의 포인터를 생각보다 이중 반복문이지만 덜한 방법으로 진행하면 문제 해결에 다가갈 것으로 보였다.
왜냐하면 투 포인트 알고리즘은 선형시간 복잡도O(n)를 가지기 때문이다.
예를 들어 그림으로 표현하면 아래와 같이 흘러간다.
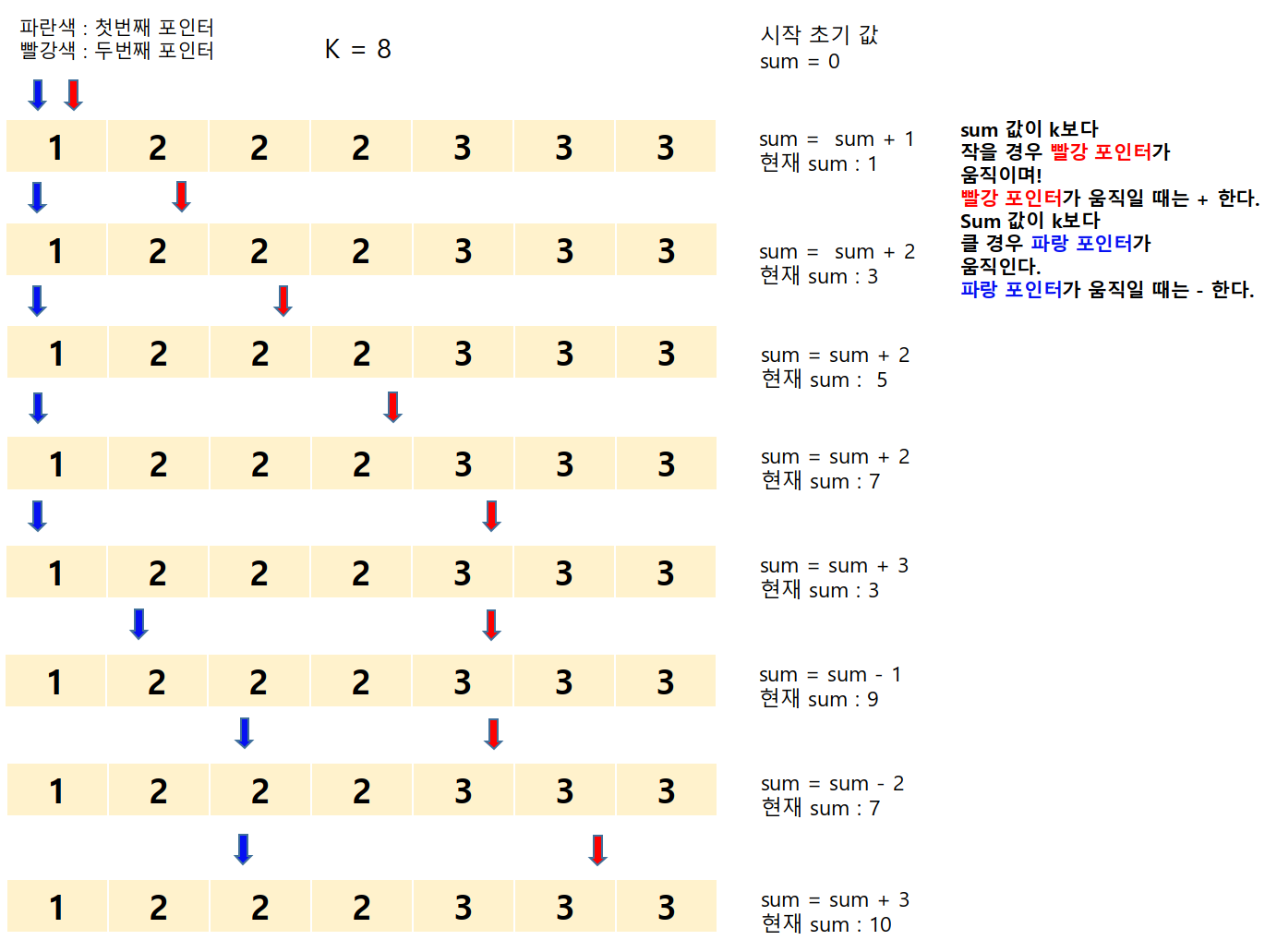

이미지가 길어서 2개로 나누었는데 확인 해보면 2 , 3 , 3 를 합계로 8이 만들어 졌고 2개의 포인터를 알아보면
파란색 포인터 : 3
빨강색 포인터 : 5
라는 값이 반환 된다.
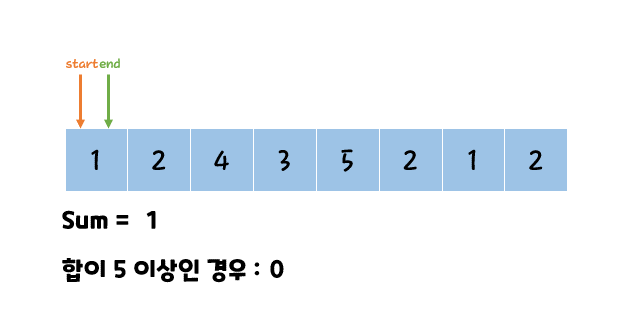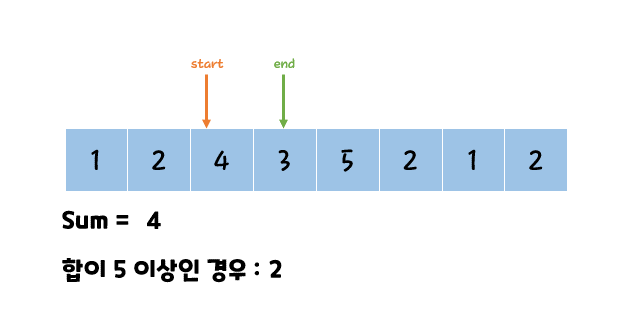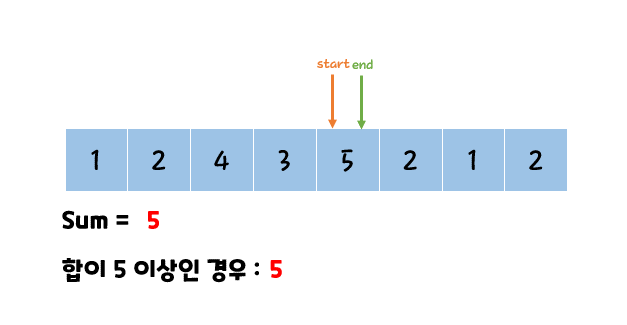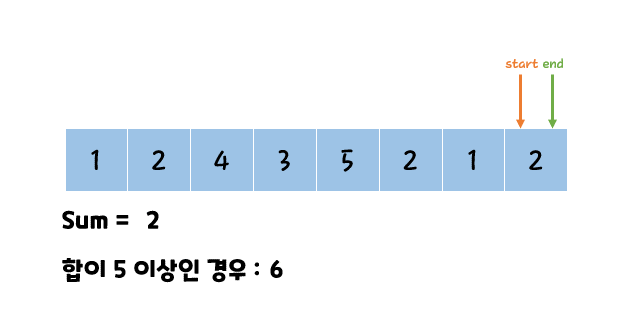
좀더 알기 쉬운 그림으로는 아래와 같다.
코드
class Solution {
public int[] solution(int[] sequence, int k) {
int[] answer = {};
// 첫번째 포인터
int startPoint = 0;
// 두번째 포인터
int lastPoint = 0;
// 합계
int sum = 0;
// 반환 포인터1
int returnPoint1 = 0;
// 반환 포인터2
int returnPoint2 = 0;
// 최소값
int min = 1000000;
// 두번째 포인터가 배열의 길이를 넘어서는 안된다.
while (lastPoint < sequence.length) {
// sum이 k보다 작을때
if (sum < k) {
sum += sequence[lastPoint];
lastPoint++;
}
// sum이 k보다 크고 첫번째 포인터가 두번째 포인터보다 작을때
while (sum > k && startPoint < lastPoint) {
sum -= sequence[startPoint];
startPoint++;
}
// sum과 k가 같을때
if (sum == k) {
// 포인터간의 최소길이를 찾기 위함
if (min > (lastPoint - 1) - startPoint) {
min = (lastPoint - 1) - startPoint;
returnPoint1 = startPoint;
returnPoint2 = (lastPoint - 1);
}
// 시작포인터에 있는 값을 sum에 감소! 다음 경우의 수를 찾기 위함
sum -= sequence[startPoint];
startPoint++;
}
}
return new int[]{returnPoint1 , returnPoint2};
}
}
마무리
오늘도 처음 사용해보는 알고리즘이 하나 생겼다. 투포인터 알고리즘... 복잡했지만 차차 적용하여 지식을 늘려가자.
'코딩 공부 > Java' 카테고리의 다른 글
| [Java] 프로그래머스 문제 - 점 찍기 (0) | 2024.08.27 |
|---|---|
| [Java] Stack를 활용한 DFS 알고리즘으로 푼 문제 (0) | 2024.08.16 |
| [Java] Comparator compare() 과 Comparable compareTo() (0) | 2024.08.06 |
| [Java] BFS(Breadth-First Search) 알고리즘이란? (0) | 2024.08.05 |
| [Java] 문제 풀다가 조금 더 깊게 DFS 알고리즘 경험 (0) | 2024.07.31 |




